摘要

用基于Cahn-Hilliard方程的相場法研究了Fe-Cr-Ni系不銹鋼中的鐵素體在熱老化和后續退火過程中調幅分解的演化過程，結果表明：在熱老化過程中調幅分解生成相連的網絡狀α‘相，調幅分解引起的Cr成分波動的波長和振幅都隨著熱老化時間的延長而增大；在隨后的退火過程中α’相逐漸溶解而Cr成分波動的振幅迅速減小，但是波長繼續增大。還討論了熱老化時的調幅分解對鐵素體納米壓痕硬度的影響以及退火溫度對調幅分解回復（α‘相溶解）所需時間的影響，結果表明：鐵素體的納米壓痕硬度主要與調幅分解的振幅有關，且隨著振幅的增大而提高。同時，提高退火溫度能顯著縮短調幅分解回復所需的時間，退火回復時間與退火溫度之間有Arrhenius形式的關系。

關鍵詞： 金屬材料 ; 調幅分解 ; 相場模型 ; 熱老化 ; 退火

Fe-Cr-Ni系不銹鋼在核能領域有重要的應用[1]。例如，308L不銹鋼焊材可用于制造壓水堆主回路接管安全端的焊接件，CF3M、CF8M和國產Z3CN20-09M等不銹鋼可用于制造主回路管道[2,3,4]。Fe-Cr-Ni系不銹鋼具有奧氏體-鐵素體混合組織，其力學性能和耐腐蝕性能良好[5,6]。但是，在工況溫度280~330℃長期服役時不銹鋼中的鐵素體會析出富Cr的α‘相和富Ni的G相[7,8,9]，使材料產生熱老化脆性[10,11,12]，成為核電站運行中嚴重的隱患[1]。將出現熱老化脆性的材料在500~600℃進行短時間（約1 h）的退火可消除α’相，降低其脆性[13,14,15]。這一發現，為延長核電站的壽命提供了有效手段[16]。

在熱老化和后續退火過程中，材料力學性能的演化與材料微觀結構的演化有密切的關系[17]。奧氏體的熱穩定性良好，在熱老化和退火過程中熱穩定性的變化很小[18,19]。材料力學性能的改變，取決于鐵素體內微觀結構的改變。當Fe-Cr-Ni系不銹鋼中鐵素體的成分和溫度位于其相圖中的調幅分解區時，鐵素體因調幅分解機制生成富Cr的α‘相和貧Cr的α相。兩相晶格錯配產生的內應力和兩相模量的差異給位錯滑移產生額外的阻力，引起材料硬化和脆化[20,21]。退火回復，則是將產生熱老化脆性的材料加熱到固溶隙上限溫度以上進行短時間保溫以使鐵素體中Cr的分布均勻化和α’相溶解，使材料的力學性能回復[16,22]。

關于鐵素體的調幅分解，已有大量的文獻。研究人員使用原子探針技術（APT）、小角度中子散射（SANS）、掃描透射電子顯微鏡（STEM）、納米壓痕（Nanoindentation）等手段，研究了Cr含量、熱老化溫度對調幅分解速度的影響，以及α‘相的結構與成分對鐵素體硬度的影響[16,23,24,25,26]。但是，調幅分解尺度只有數納米以及α’相與基體之間沒有足夠的襯度區分，影響實驗的準確表征[23]。同時，熱老化實驗的時間成本和金錢成本非常高昂。Pareige等[7]發現：經過二十余年服役狀態熱老化，調幅分解仍然處在初期階段；即使是在400℃的加速熱老化實驗，也需要數萬小時才能完成[27]。

計算模擬能快速、實時地反映材料的微觀組織轉變，提供了一種高效、經濟的研究手段。基于Cahn-Hilliard方程[28]的相場法是研究調幅分解的模擬方法之一。用相場法可解釋Fe-Cr模型合金調幅分解的實驗結果[29,30,31]。盡管Fe-Cr-Ni系不銹鋼中鐵素體的成分遠比模型合金復雜，在α‘-α兩相界面處有G相析出，并且G相和調幅分解之間的協同作用[7]可能影響調幅分解的演化速度，但是鐵素體調幅分解的機制與Fe-Cr模型合金的調幅分解機制相同[32]。Chung等[33]發現，退火后材料的調幅分解結構消失而G相仍存在，但是其硬度和塑性明顯回復。這表明，調幅分解是產生熱老化脆性的主要原因，而影響較小的G相屬于次要原因。另外，在現有模型中難以直接引入G相并考慮其對調幅分解的影響。因此，本模型主要考慮調幅分解的演化，而忽略G相的演化。但是，為了使Fe-Cr相場模型更好地模擬實際鐵素體的調幅分解，用Fe-Cr-Ni正規溶液自由能替代Fe-Cr正規溶液自由能以考慮Ni對Fe-Cr固溶隙寬度的影響；同時，還引入擴散系數的調整因子來修正Ni、Si等其他合金元素和G相對調幅分解演化速度的影響[34]。

本文基于包含Cahn-Hilliard方程的相場法，使用文獻中的熱力學數據模擬Fe-Cr-Ni系不銹鋼中鐵素體在熱老化以及后續退火過程中調幅分解的演變，討論熱老化后鐵素體的納米壓痕硬度隨調幅分解振幅的變化規律以及退火溫度對調幅分解回復（α’相溶解）所需時間的影響。

1 相場模型

1.1 自由能表達

體系總的自由能F包括化學能和應變能，可表示為[28]

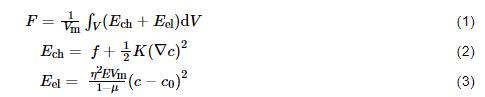
其中，V_m為不銹鋼的摩爾體積，假定其為常數；V為體系的體積；E_ch為化學能密度，f為Gibbs自由能密度，K為Cr濃度的梯度能系數，c為Cr的濃度；E_el為彈性能密度，η為單位Cr濃度引起的鐵素體晶格常數變化的系數，E為楊氏模量，μ為泊松比，c₀為鐵素體內Cr的平均濃度。

Fe-Cr-Ni系不銹鋼鐵素體中主要的合金元素是Cr和Ni[19]。因為Ni會改變固溶隙寬度[34]，直接使用Fe-Cr正規溶液自由能可能引入較大的偏差，因此本工作使用Fe-Cr-Ni正規溶液自由能。由于Ni參與G相的形成，而本模型忽略G相的演化，故將Ni的濃度設為常量（僅代入f的表達式，但不求解）。于是f可表示為[35]

假定K只與Fe-Cr相互作用系數相關，其表達式為[35]

式中，為原子間距。

1.2 控制方程

α相和α‘相同屬于鐵素體，其晶格結構相同而Cr含量不同，Fe-Cr調幅分解的動力學過程實際上是Cr的擴散過程，特別是上坡擴散過程。因此，控制方程只使用描述Cr濃度場演化的Cahn-Hilliard方程[28]

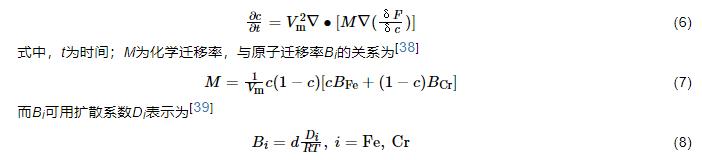
Fe-Cr-Ni系不銹鋼的成分遠比Fe-Cr模型合金復雜，如果直接使用Fe-Cr互擴散實驗[40]給出的擴散系數Di，得到的模擬結果會明顯滯后于文獻[19]中熱老化和退火的實驗結果。產生這種差異的原因可能有：Ni、Si等其他合金元素促進Fe、Cr的擴散[41]，G相加速調幅分解波長、振幅隨時間的演化[7]，以及更高溫度下測定的擴散系數同熱老化、退火溫度下的擴散系數真值之間存在偏差。因此，本文參照文獻[42]的方法在式（8）中引入調整因子d。通過改變擴散速度調整調幅分解波長、振幅隨時間的演化速度，使模擬結果與實驗結果一致。根據文獻[19]熱老化7000 h和后續退火1 h的實驗結果，d的取值標定為10.7。這樣，標定后的物理模型可在實驗點以外作適當的模擬預測。

1.3 模擬條件

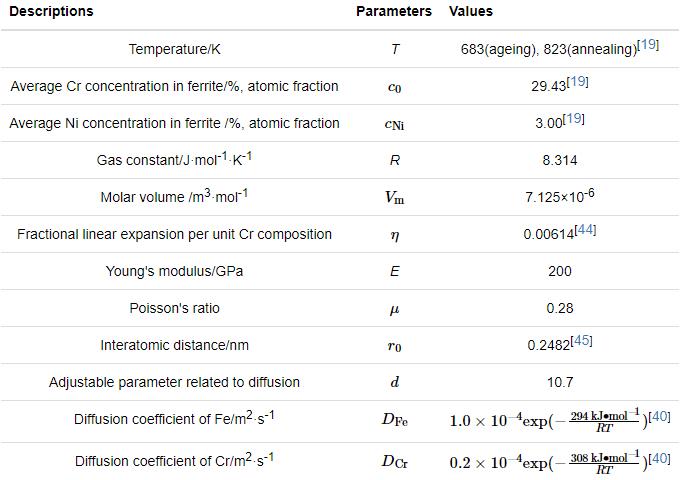
本文建立了一個尺寸為30 nm×30 nm×60 nm的三維模擬區域，控制方程為偏微分方程，采用有限單元法（FEM）[43] 求解，單元為0.5 nm×0.5 nm×0.5 nm的六面體，時間步長為0.001 h，邊界條件為Neumann邊界條件。先模擬在410℃下熱老化7000 h的演化，之后升溫到550℃模擬退火1 h的演化；Cr的初始濃度及其波動范圍、Ni的平均濃度都與文獻[19]中308L不銹鋼的實驗數據相同。模擬參數的設定列于表1，表1中和隨溫度的變化與f和Di隨溫度的變化相比很小，因此在本模擬中設這些參數與溫度無關。

表1   相場模型使用的參數值

2 模擬結果

圖1給出了相場模擬的熱老化和退火過程中不同時間Cr的分布。采用略高于平均Cr濃度的35%為等濃度面作圖[19]，以其作為α’和α的相界面則等濃度面包圍的區域為α‘相，外部為α相。圖1a1中相場模型初始狀態的Cr分布和圖2a中未熱老化樣品的實驗結果都表明：在熱老化之前樣品中原本就存在Cr濃度高于35%的顆粒狀團簇，在基體中隨機分布。在410℃熱老化后（圖1a2~a5）已有的α’相隨著調幅分解的進行逐漸長大，并產生新的α‘相。這些α’相漸漸相連，形成調幅分解標志性的網絡狀結構。之后，設定模擬溫度為550℃模擬退火過程（實驗中，樣品到溫入爐后很快達到退火溫度，升溫時間與退火時間相比很短，故在模擬中忽略升溫過程的影響）。如圖1b1~b5所示，可見α‘相逐漸溶解，調幅分解的網絡結構消失，而未熱老化時Cr含量較高的團簇在退火過程中需要更長的時間才能溶解。模擬結果表明，經過1.23 h的退火后（圖1b4）Cr成分波動的振幅恢復到初始值（5.21%），2.35 h后（圖1b5）Cr濃度高于35%的α’相完全溶解。分別對比熱老化7000 h的模擬結果（圖1a5）與實驗結果（圖2b）和退火1 h的模擬結果（圖1b3）與實驗結果（圖2c），可見相場模型良好地復現了308L中鐵素體在熱老化及退火過程中調幅分解的演化（圖2a和2c中，α‘相在樣品頂端有部分聚集，可能是樣品中Cr濃度分布不均勻所致）。

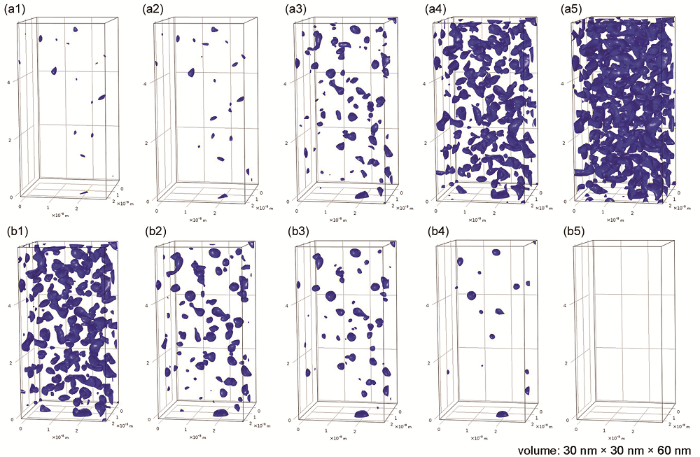
圖1   模擬的熱老化和退火不同時間的Cr濃度分布，圖中的等值面為35% Cr（原子分數）

圖2   文獻[19]中APT實驗測得的Cr元素分布

為了與實驗一維成分分布的結果對比，提取模型高度方向一條直線上Cr的濃度數據，并分析其頻率分布，結果如圖3所示。模擬與實驗的一維成分分布曲線（圖3a）有相似的波長和振幅。盡管退火后實驗曲線（圖3a3藍色實線）的波長明顯小于模擬曲線，但是平滑后（圖3a3紅色實線）則與模擬曲線的波長接近。對比模擬與實驗的頻率分布曲線（圖3b），可見兩者頻率分布曲線的形式大致相同：未熱老化時模擬和實驗的Fe、Cr濃度頻率分布都滿足二項分布（Binomial frequency distribution）；熱老化7000 h后都偏離二項分布，且在高Cr（低Fe）濃度范圍內的頻率分布增加；退火1 h后，又恢復二項分布。但是模擬和實驗的頻率分布曲線也有一定差別——模擬的濃度分布更加集中，并且Fe的曲線整體向高濃度方向偏移。模擬的濃度分布比實驗更加集中，其主要原因是APT需要對包含一定原子數量的區塊進行采樣統計取平均，得到的濃度值不連續并且其變化可能比真實情況更加平緩[46]；Fe的曲線整體向高濃度方向偏移的主要原因則是，若保持Cr、Ni濃度分別與308L鐵素體中Cr、Ni濃度一致，則其他合金元素都將計為Fe的濃度，自然引起Fe的模擬曲線整體向高濃度方向偏移。

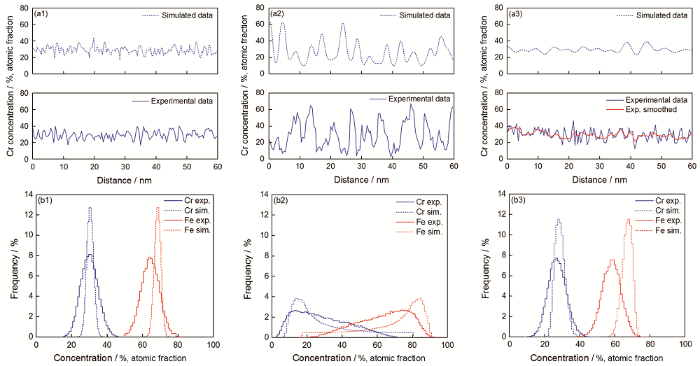
圖3   模擬的Cr一維成分分布、頻率分布與實驗結果[19]的對比

3 討論

3.1 調幅分解的波長、振幅隨著熱老化和退火時間的變化

調幅分解的波長（λ），是Cr濃度峰值點到下一個峰值點的平均距離，可由一維成分曲線的自相關分析（Autocorrelation analysis）得到[46]。取圖3中數據的采樣直線上不同時間的一維成分分布進行自相關分析，得到調幅分解的波長隨熱老化和退火時間的變化，如圖4所示。在熱老化過程中，模擬和實驗得到的波長都隨著時間的延長而增大，模擬曲線的形式與文獻[46]的模擬結果類似。在退火過程中，由于溫度位于固溶隙以外α’相溶解、Cr濃度均勻化，波長應該隨著退火的進行而增大。但是，退火后的實驗曲線（圖3a3藍色實線）甚至比未經熱老化的實驗曲線（圖3a1）波長更小，說明退火后成分分布曲線的波動可能是APT自身的波動所致。將實驗曲線平滑處理后（圖3a3紅色實線），再進行自相關分析得到的波長值為6.00 nm，與模擬值5.42 nm接近。

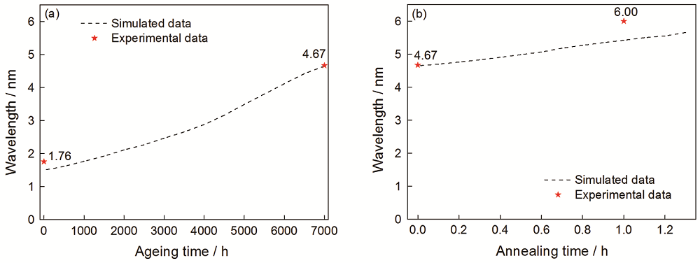
圖4   模擬的調幅分解波長隨著熱老化時間和退火時間的變化，圖中星形為308L不銹鋼的實驗結果[19]

調幅分解的振幅（A），是α‘和α兩相的平均Cr濃度之差[46]，其隨著熱老化和退火時間的變化如圖5所示。在熱老化過程中模擬曲線呈“S型”增長，表明調幅分解經歷了慢-快-慢的演變過程，曲線形式與文獻[46]的模擬結果類似。退火時較高的溫度顯著提高了Fe、Cr的擴散速度，振幅很快地降低，1 h的模擬值為6.69%，與實驗值6.62%接近。

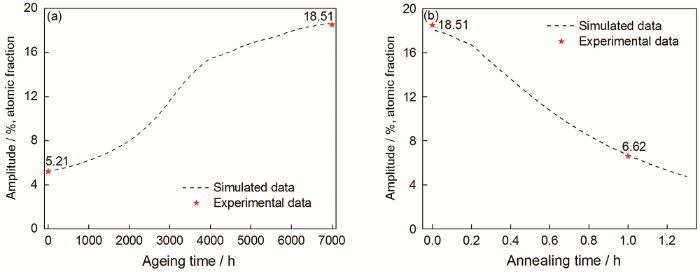
圖5   模擬的調幅分解的振幅隨熱老化時間和退火時間的變化，圖中的星形為308L不銹鋼的實驗結果[19]

本文的模型也適用于模擬其他Fe-Cr-Ni系不銹鋼鐵素體的調幅分解。調整模型中Cr的初始濃度、波動范圍、Ni的平均濃度以及熱老化溫度，同文獻[7]中CF3M雙相鋼的實驗數據一致，并模擬CF3M中鐵素體調幅分解波長、振幅的演化（圖6）。模擬結果與實驗的結果接近，表明模型具備較大的適用范圍。對比圖6和圖4a、圖5a，可見熱老化溫度降低、Cr濃度下降顯著減慢調幅分解的演化，與調幅分解的一般規律相符。

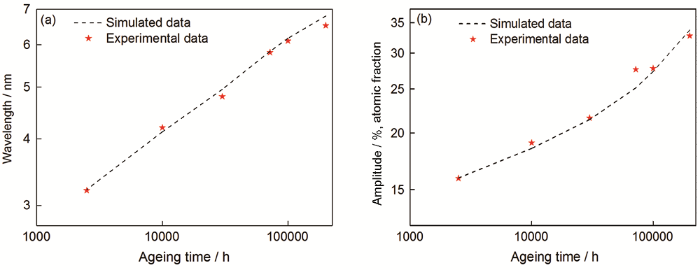
圖6   模擬的調幅分解波長和振幅隨熱老化時間的變化，圖中星形為CF3M雙相鋼的實驗結果[7]。注意此處=27.38%（原子分數），=5.42%（原子分數），T=623 K

3.2 調幅分解振幅與鐵素體納米壓痕硬度的關系

熱老化時鐵素體發生調幅分解，其屈服強度和硬度升高而韌性降低；奧氏體難以發生調幅分解，其力學性能變化較小。因此，Fe-Cr-Ni系不銹鋼的宏觀力學性能取決于兩相的比例，例如：以鐵素體為主的S2205鋼的屈服強度隨熱老化的進行顯著升高[22]；以奧氏體為主的308L、Z3CN20-09M鋼的屈服強度隨熱老化的進行只略微升高[3,47]。

Lin等[48]使用納米壓痕測定了文獻[19]中同一308L不銹鋼樣品的鐵素體在不同熱老化時間后的硬度變化。結果表明，鐵素體的硬度隨熱老化時間呈“S型”增長，其形狀（圖7中的紅色實線）與圖5中調幅分解的振幅變化曲線類似。對此，本文簡要探討調幅分解的振幅同鐵素體的納米壓痕硬度（）的關系。Kato[20]和Park[21]基于連續介質力學理論，提出了用于解釋調幅分解對鐵素體屈服強度影響的Kato-Park模型

式中第一項為α’相和α相晶格錯配對鐵素體屈服強度的貢獻，第二項為兩相模量差異的貢獻，

為鐵素體屈服強度增量，m為泰勒因子（m=3.06），A為調幅分解的振幅，為單位Cr濃度引起的鐵素體晶格常數變化的系數，Y與楊氏模量E相關（，μ為泊松比），b為位錯Burgers矢量的模，為調幅分解的波長。若各參數取值同表1并以初始狀態的鐵素體屈服強度為基準，將模擬得到的熱老化不同時間的A、值代入式（9），可計算出鐵素體屈服強度增量，如圖7中的虛線所示。

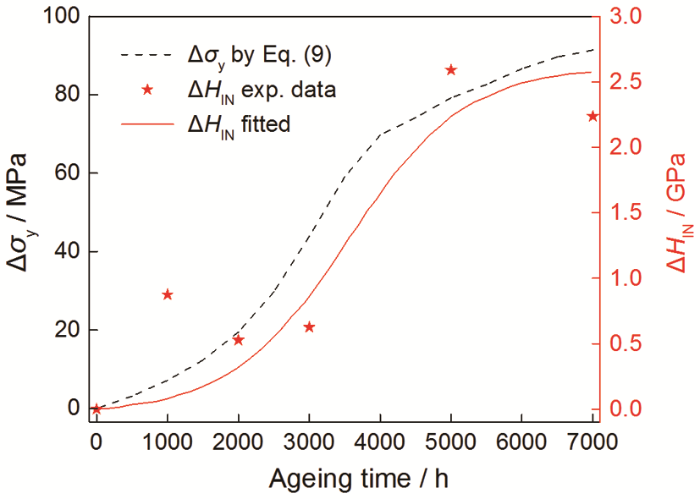
圖7   使用式（9）計算出的鐵素體屈服強度增量和文獻[48]中鐵素體納米壓痕硬度增量與熱老化時間的關系

從式（9）中可以看出，

主要受A的影響，兩者之間呈正相關，而的影響較小[21]。另外，有研究[49,50]表明，在雙相鋼的鐵素體中有如下近似關系：

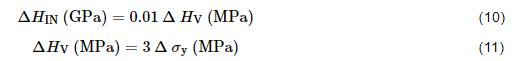
式中 為鐵素體納米壓痕硬度增量，為鐵素體維氏硬度增量，為鐵素體屈服強度增量。顯然有：

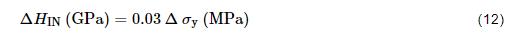
由此可見，也主要受A的影響，且隨著A的增大而增大。式（12）的近似關系也反映在圖7中，這就解釋了為何鐵素體的納米壓痕硬度隨時間的變化曲線同調幅分解的振幅隨時間的變化曲線相似，同時這種相似性從側面反映了本工作相場模型的有效性。

3.3 退火溫度對調幅分解回復所需時間的影響

鑒于模型與實驗結果[7,19]符合較好，計算了不同熱老化時間（0~20000 h）后308L不銹鋼鐵素體在不同退火溫度（500～600℃）回復到初始狀態（以振幅下降到初始值5.21%為判斷標準）所需要的退火時間，結果如圖8a所示。熱老化2500~5000 h后退火回復時間顯著提高，5000 h后曲線逐漸趨于平緩。如圖5a所示，調幅分解的振幅在2500~5000 h之間迅速增大，5000 h后則緩慢增大。因此，以振幅下降到初始值為判斷標準的退火回復時間，具有相似的變化趨勢。并且，提高退火溫度能顯著縮短退火回復時間。其原因是，溫度越高熱激活越顯著，擴散系數越大。研究表明，不銹鋼中的熱激活過程服從Arrhenius形式的關系式[14,51]

其中，分別為溫度下達到相同狀態所需的時間，Q為相應的激活能，R為理想氣體常數。圖8a中以退火回復時間的自然對數為縱坐標時，不同溫度的曲線近似平行，與式（13）的形式相符。為了進一步確定退火回復時Q的取值，取熱老化不同時間后退火回復時間的自然對數對退火絕對溫度的倒數作圖（圖8b），使用線性回歸得到直線斜率的平均值為38031 K，進而計算出

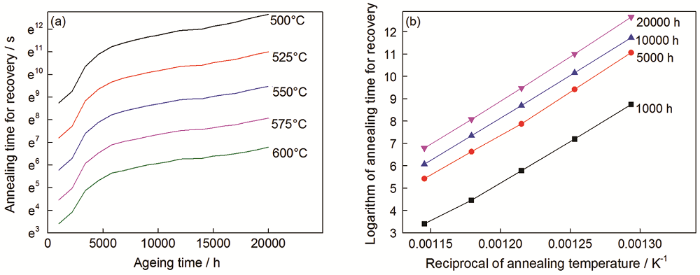
圖8   模擬的不同退火溫度下回復到初始狀態所需要的退火時間隨熱老化時間的變化，以及熱老化不同時間后退火回復時間的自然對數同退火絕對溫度的倒數的關系

4 結論

（1） 以Fe-Cr-Ni正規溶液自由能為基礎建立的Fe-Cr相場模型，標定參數后能良好地描述Fe-Cr-Ni系不銹鋼中鐵素體在熱老化和退火過程中調幅分解的演化。

（2） 模擬與實驗結果符合得很好：熱老化引起鐵素體的調幅分解，生成彼此相連的網絡狀α‘相；Cr成分波動的波長和振幅都隨著熱老化時間的延長而增大；退火使α’相完全溶解，Cr成分波動的振幅隨之降低而波長繼續增大。

（3） 熱老化后鐵素體的納米壓痕硬度主要受調幅分解振幅影響，因為屈服強度與振幅正相關（Kato-Park模型），而納米壓痕硬度增量與其屈服強度增量之間又存在近似的正比關系。

（4） 提高退火溫度可顯著降低調幅分解回復（α‘相溶解）所需的時間。熱老化相同時間后在不同溫度下退火達到相同的退火回復狀態，需要的時間與退火溫度之間存在Arrhenius形式的關系。

參考文獻

[1] Zhang B, Xue F, Li S L, et al. Non-uniform phase separation in ferrite of a duplex stainless steel [J]. Acta Mater., 2017, 140: 388

[2] Dong L, Han E H, Peng Q J, et al. Environmentally assisted crack growth in 308L stainless steel weld metal in simulated primary water [J]. Corros. Sci., 2017, 117: 1

[3] Brooks J A, Thompson A W. Microstructural development and solidification cracking susceptibility of austenitic stainless steel welds [J]. Int. Mater. Rev., 1991, 36(1): 16

[4] Wang W, Luo K L, Lu Y H. Microstructure of welding seam and its effect on propagation of microcracks in nuclear grade Z3CN20-09M stainless steel [J]. Chin. J. Mater. Res., 2014, 28(11): 809

[4] (王瑋, 羅奎林, 陸永浩. 核級不銹鋼Z3CN20-09M焊縫組織及對裂紋擴展的影響 [J]. 材料研究學報, 2014, 28(11): 809)

[5] Vitek J M, David S A, Alexander D J, et al. Low temperature aging behavior of type 308 stainless steel weld metal [J]. Acta Mater., 1991, 39(4): 503

[6] Takeuchi T, Kameda J, Nagai Y, et al. Study on microstructural changes in thermally-aged stainless steel weld-overlay cladding of nuclear reactor pressure vessels by atom probe tomography [J]. J. Nucl. Mater., 2011, 415(2): 198

[7] Pareige C, Novy S, Saillet S, et al. Study of phase transformation and mechanical properties evolution of duplex stainless steels after long term thermal ageing (>20 years) [J]. J. Nucl. Mater., 2011, 411(1-3): 90

[8] Vitek J M. G-phase formation in aged type 308 stainless steel [J]. Metall. Mater. Trans. A, 1987, 18(1): 154

[9] Danoix F, Auger P. Atom probe studies of the Fe-Cr system and stainless steels aged at intermediate temperature: a review [J]. Mater. Charact., 2000, 44(1-2): 177

[10] Soriano-Vargas O, Avila-Davila E O, Lopez-Hirata V M, et al. Effect of spinodal decomposition on the mechanical behavior of Fe-Cr alloys [J]. Mater. Sci. Eng. A, 2010, 527(12): 2910

[11] Chung H M, Leax T R. Embrittlement of laboratory and reactor aged CF3, CF8, and CF8M duplex stainless steels [J]. Mater. Sci. Technol., 1990, 6(3): 249

[12] Guo X F, Ni Y Y, Gong J M, et al. Formation of G-phase in 20Cr32Ni1Nb stainless steel and its effect on mechanical properties [J]. Acta Metall. Sin. (Engl. Lett.), 2017, 30(9: 829

[13] Mateo A, Palomino J L, Salan N, et al. Mechanical evaluation of a reversion heat treatment for a duplex stainless steel thermally embrittled [A]. Proceedings of the 11th Biennial European Conference on Fracture [C]. Warley, 1996

[14] Chung H M. Aging and life prediction of cast duplex stainless steel components [J]. Int. J. Pres. Ves. Pip., 1992, 50(1-3): 179

[15] Konosu S. Effect of reversion heat treatments on the mechanical properties of a 13% Cr steel subjected to 475℃ embrittlement [J]. Scr. Mater., 1992, 26(10): 1631

[16] Li S L, Zhang H L, Wang Y L, et al. Annealing induced recovery of long-term thermal aging embrittlement in a duplex stainless steel [J]. Mater. Sci. Eng. A, 2013, 564: 85

[17] Ding X P, Liu X, He Y L, et al. Evolution of precipitated phase during aging treatment in 316L austenitic stainless steel [J]. Chin. J. Mater. Res., 2009, 23(3): 269

[17] (丁秀平, 劉雄, 何燕霖等. 316L奧氏體不銹鋼中時效條件下析出相演變行為的研究 [J]. 材料研究學報, 2009, 23(3): 269)

[18] Takeuchi T, Kameda J, Nagai Y, et al. Microstructural changes of a thermally aged stainless steel submerged arc weld overlay cladding of nuclear reactor pressure vessels [J]. J. Nucl. Mater., 2012, 425(1-3): 60

[19] Lin X D, Peng Q J, Han E H, et al. Effect of annealing on microstructure of thermally aged 308L stainless steel weld metal [J]. Acta Metall. Sin., 2019, 55(5): 555

[19] (林曉冬, 彭群家, 韓恩厚等. 退火對熱老化308L不銹鋼焊材顯微結構的影響 [J]. 金屬學報, 2019, 55(5): 555) doi: 10.11900/0412.1961.2018.00365

[20] Kato M. Hardening by spinodally modulated structure in bcc alloys [J]. Acta Mater., 1981, 29(1): 79

[21] Park K H, LaSalle J C, Schwartz L H, et al. Mechanical properties of spinodally decomposed Fe-30wt% Cr alloys: Yield strength and aging embrittlement [J]. Acta Mater., 1986, 34(9): 1853

[22] Shamanth V, Ravishankar K S. Dissolution of alpha-prime precipitates in thermally embrittled S2205-duplex steels during reversion-heat treatment [J]. Results Phys., 2015, 5: 297

[23] Xu X, Westraadt J E, Odqvist J, et al. Effect of heat treatment above the miscibility gap on nanostructure formation due to spinodal decomposition in Fe-52.85 at% Cr [J]. Acta Mater., 2018, 145: 347

[24] Ujihara T, Osamura K. Kinetic analysis of spinodal decomposition process in Fe-Cr alloys by small angle neutron scattering [J]. Acta Mater., 2000, 48(7): 1629

[25] Leax T R, Brenner S S, Spitznagel J A. Atom probe examination of thermally ages CF8M cast stainless steel [J]. Metall. Mater. Trans. A, 1992, 23(10): 2725

[26] Danoix F, Auger P, Chambreland S, et al. A 3D study of G-phase precipitation in spinodally decomposed α-ferrite by tomographic atom-probe analysis [J]. Microsc. Microanal. Microstruct., 1994, 5(2): 121

[27] Fujii K, Fukuya K. Effects of radiation on spinodal decomposition of ferrite in duplex stainless steel [J]. J. Nucl. Mater., 2013, 440(1-3): 612

[28] Cahn J W. On spinodal decomposition [J]. Acta Mater., 1961, 9(9): 795

[29] Miller M K, Hyde J M, Hetherington M G, et al. Spinodal decomposition in Fe-Cr alloys: Experimental study at the atomic level and comparison with computer models-I. Introduction and methodology [J]. Acta Mater., 1995, 43(9): 3385

[30] Li Y S, Li S X, Zhang T Y. Effect of dislocations on spinodal decomposition in Fe-Cr alloys [J]. J. Nucl. Mater., 2009, 395(1-3): 120

[31] Li Y S, Zhu H, Zhang L, et al. Phase decomposition and morphology characteristic in thermal aging Fe-Cr alloys under applied strain: A phase-field simulation [J]. J. Nucl. Mater., 2012, 429(1-3): 13

[32] Emo J, Pareige C, Saillet S, et al. Kinetics of secondary phase precipitation during spinodal decomposition in duplex stainless steels: A kinetic Monte Carlo model - Comparison with atom probe tomography experiments [J]. J. Nucl. Mater., 2014, 451(1-3): 361

[33] Theus G J, Weeks J R. Environmental Degradation of Materials in Nuclear Power Systems-Water Reactors [M]. Pennsylvania: The Metallurgical Society of AIME, 1988

[34] Miller M K, Anderson I M, Bentley J, et al. Phase separation in the Fe-Cr-Ni system [J]. Appl. Surf. Sci., 1996, 94: 391

[35] Cahn J W, Hilliard J E. Free energy of a nonuniform system. I. Interfacial free energy [J]. J. Chem. Phys., 1958, 28(2): 258

[36] Dinsdale A T. SGTE data for pure elements [J]. CALPHAD, 1991, 15(4): 317

[37] Miettinen J. Thermodynamic reassessment of Fe-Cr-Ni system with emphasis on the iron-rich corner [J]. CALPHAD, 1999, 23(2): 231

[38] Andersson J O, Agren J. Models for numerical treatment of multicomponent diffusion in simple phases [J]. J. Appl. Phys., 1992, 72(4): 1350 doi: 10.1063/1.351745

[39] Wheeler A A, Boettinger W J, McFadden G B. Phase-field model for isothermal phase transitions in binary alloys [J]. Phys. Rev. A, 1992, 45(10): 7424 doi: 10.1103/PhysRevA.45.7424

[40] Dieter G E, Bacon D J. Mechanical Metallurgy [M]. New York: McGraw-Hill, 1986

[41] Rothman S J, Nowicki L J, Murch G E. Self-diffusion in austenitic Fe-Cr-Ni alloys [J]. J. Phys. F, 1980, 10(3): 383

[42] Honjo M, Saito Y. Numerical simulation of phase separation in Fe-Cr binary and Fe-Cr-Mo ternary alloys with use of the Cahn-Hilliard equation [J]. ISIJ Int., 2000, 40(9): 914.

[43] COMSOL Multiphysics software. Version 5.3. Stockholm (Sweden): COMSOL Inc. 2017

[44] Mehrer H, Stolica N. Diffusion in Solid Metals and Alloys [M]. Berlin: Springer, 1990

[45] Pareige C, Emo J, Saillet S, et al. Kinetics of G-phase precipitation and spinodal decomposition in very long aged ferrite of a Mo-free duplex stainless steel [J]. J. Nucl. Mater., 2015, 465: 383

[46] Hyde J M, Miller M K, Hetherington M G, et al. Spinodal decomposition in Fe-Cr alloys: Experimental study at the atomic level and comparison with computer models-II. Development of domain size and composition amplitude [J]. Acta Mater., 1995, 43(9): 3403

[47] Li S, Wang Y, Li S, et al. Microstructures and mechanical properties of cast austenite stainless steels after long-term thermal aging at low temperature [J]. Mater. Des., 2013, 50: 886

[48] Lin X, Peng Q J, Han E H, et al. Assessment of thermal aging of austenitic stainless steel weld metal by using the double loop electrochemical potentiokinetic reactivation technique [J]. Corrosion, 2018, 75(4): 377

[49] Liu X, Wang R, Ren A, et al. Evaluation of radiation hardening in ion-irradiated Fe based alloys by nanoindentation [J]. J. Nucl. Mater., 2014, 444(1-3): 1

[50] Tabor D. The physical meaning of indentation and scratch hardness [J]. Br. J. Appl. Phys., 1956, 7(5): 159

[51] Pumphrey P H, Akhurst K N. Aging kinetics of CF3 cast stainless steel in temperature range 300~400℃ [J]. Mater. Sci. Technol., 1990, 6(3): 211 doi: 10.1179/mst.1990.6.3.211